I have been thinking about emergent properties lately, given abilities large language models exhibit that are hard to explain from the nature of their architecture and training alone. To experiment with such properties, we will be using a simpler device than the typical neuron found in artificial neural networks, which in turn are simplifications of those found in biological neural networks. The device I have in mind is something I will call a bulb.
- A bulb is a device with two states, on and off.
While simple, I will show how under the right conditions even bulbs have emergent properties, and reason why such emergent properties can persist over time.
System of a Bulb
Is a bulb a system? It can be, although a system is quite more complicated than a bulb alone. Let us first try to define a generic system in its simplest form.
- A system is a construct that persists over some time with properties that can be reliably measured.
By saying that a system is a construct we imply that it is possible to describe what constitutes the system. It persists over time, such that we would still refer to the system as the system after some time has passed, even if it may have undergone changes in the meantime. To reliably measure its properties means that the possible margins of error are within acceptable limits and that the results of those measurements are understandable in some context.
This also means that there is a who in the system. Someone put together the description of the system. Someone identifies a system as being the same or sufficiently changed to be a new system. Someone performs measurements and evaluates the results. And, for complex systems there are usually many such people involved. Therefore, it is very hard to completely remove all subjective aspects of a system. With that in mind, the description of our first experimental system is as follows.
- A system of a bulb is a system containing exactly one bulb whose state can be measured.
For the sake of the experiment, we will also introduce Archie and Bella who will interact with the system.
Investigating a System of a Bulb
Archie and Bella will take turns interacting with three systems of a bulb, where each interaction consists of measuring the state of the bulb. Here are the results of eight measurements for the first system.

After discussing their measurements, they conclude that the bulb is and remains off for the duration of the experiment. If there is anything happening in this system, it is happening more rarely than this experiment could capture.
Moving on to the second system, they get the following results.

Archie is pretty sure that it is a system similar to the first one, whereas Bella now gets a completely different result. However, after seeing the results in a table like this they form a hypothesis about the system that explains both their measurements. The hypothesis is that measuring the state of the bulb also changes its state. When Archie measures off the bulb turns on and when subsequently Bella measures on the bulb turns off. Such a system carries a very simple memory of its last interaction, with a fully predictable next state.
Finally, measuring the third system, Archie and Bella get these results.

The results are inconclusive. Debating these, Archie and Bella come up with several possible explanations.
- The system is similarly affected by measurements, but there is a third party involved and interfering with their measurements.
- The system is by unknown means conveying some kind of message, using the state of the bulb to do so.
- The system is susceptible to random disturbances, making the bulb uncontrollably go on or off.
These all illustrate complexities of systems. The behavior of a system may be hard to determine if it can be affected by the people using it and there is little control of when, how, and by whom it is being used. It is also hard if there are parts of the system that are “black boxes” to the ones trying to determine the behavior, even when there is some underlying logic to them. If also randomness is allowed to play a part in the behavior, it may be impossible to distinguish what is caused by interference, by underlying unknown logic, or by random choice.
I believe all of these complexities apply to many LLMs.
Bright and Dull Systems
While a surprising number of things can be concluded from a system of a bulb, even more can be said if we allow for several bulbs in a system.
- A system of many bulbs is a system containing more than one bulb whose individual states can be measured.
Once there are several bulbs in a system, such a system can gain properties that the individual bulbs do not have by themselves. In particular, we will look at a property defined as:
- The atmosphere of a system of many bulbs is called bright if more than half of the bulbs are on, and dull otherwise.
Given that the bulbs alone cannot be bright or dull, the atmosphere can be said to be an emergent property of the system. For the sake of brevity, we will introduce the notation S(n) for a system of many bulbs containing n bulbs. Why S(2) is too dull to investigate will be left to the reader as an exercise.
Investigating Systems of Many Bulbs – S(3)
We will start by looking at S(3). After investigating the systems of a bulb, both Archie and Bella have gained a preference for bulbs that are on. They will therefore do what they can, through interactions with S(3) to keep it bright. The third system of a bulb with inconclusive results made them weary about systems in general though. What will it take for S(3) to remain bright?
Archie and Bella come up with a strategy. They will prime S(3) so that all bulbs are on, then figure out the minimal amount of work needed to ensure that it remains bright even if some bulbs go off. They draw the following schematic, depicting all possible state changes for individual bulbs for the first three changes made. The schematic represents the bulbs in the system as bits, with 1 for on and 0 for off.
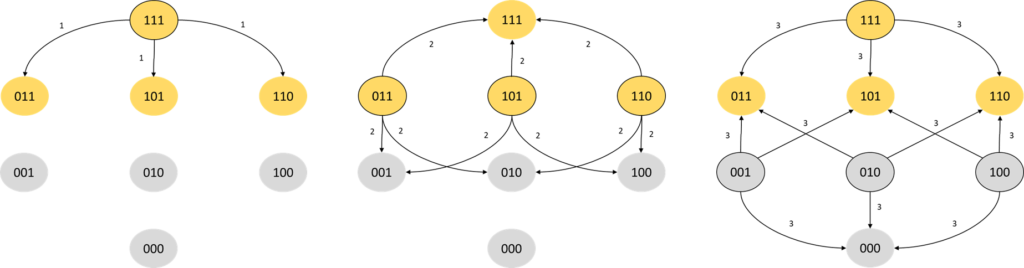
After the first bit flip we are guaranteed to stay in a bright state. At the second flip, one third of the flips will take us to a bright state, and at the third flip, three quarters of the flips take us to a bright state. There are, however, equally many dull states.
If this system is left to its own devices and there is no preference for a bright atmosphere, it seems natural that after some time and interactions the initial bright state will be “erased”, and the probability of finding a bright atmosphere is the same as finding a dull one. We might as well have tossed a coin. Work is therefore needed to maintain the bright atmosphere.
The least amount of work can be achieved if it is possible to detect the first bulb switching off and immediately rectify this by turning it on again, so that all bulbs stay on. Archie and Bella are worried that S(3) will require constant monitoring in order to maintain a bright atmosphere, given that they would have to rectify a system going dull so quickly.
Investigating Systems of Many Bulbs – S(11)
S(3) does not have a particularly resilient atmosphere, even if it starts out as completely bright. It is a very small system, though. So instead, Archie and Bella decide to look at an upgrade, S(11), which if started completely bright can guarantee a bright atmosphere for up to five flips. With 11 bulbs, at least six have to be switched off for the system to go dull, so the time to react if a dull-loving troll gets their hands on the system is extended.
But what if the system is susceptible to random disturbances? After six random successive flips dullness is not certain, as we know from S(3) that sometimes the same bulb will be flipped twice, leading us back to a bright atmosphere. There must be a probability that it remains bright under chaotic circumstances.
Already for S(11) the math gets thorny, and Markov Chains have to be used, leading to large stochastic matrices that need to be multiplied with a vector in order to get the actual probability. While there are closed form solutions to the problem, Archie and Bella would like to understand the long term behavior under chaotic circumstances and none of them are qualified to do the math. Since an approximate result will suffice, they call their programmer friend who quickly wraps up a program that estimates the probabilities.
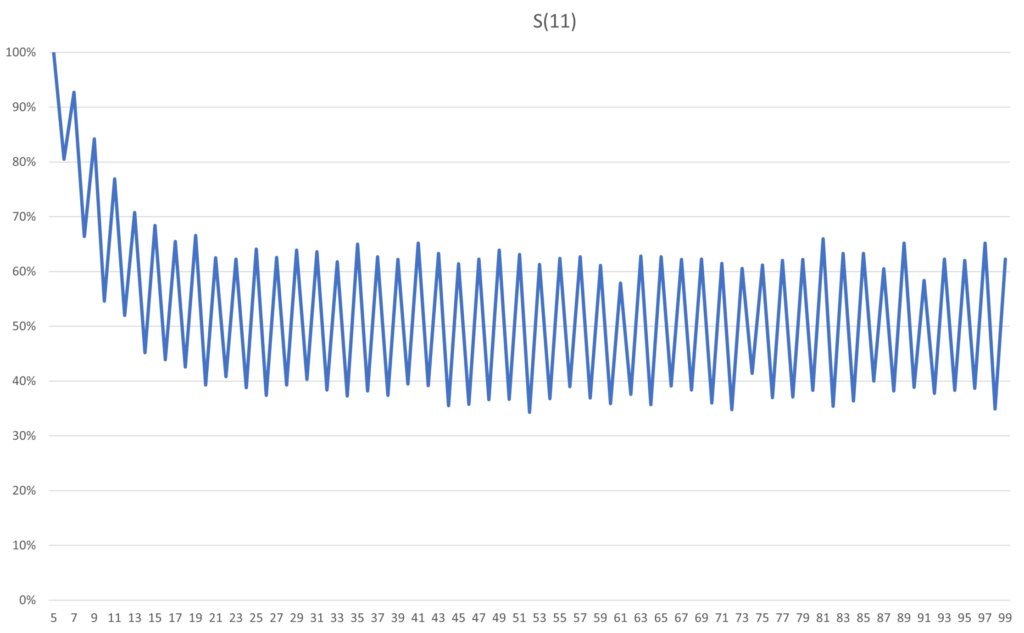
As expected, after five flips S(11) is 100% probable to remain bright. However, erasure happens quickly after the fifth flip, with a steep decline in probability. After about 18 flips it is just as likely that the atmosphere of the system is dull as it is bright. Given that there is already a 20% risk of dullness on the sixth flip, you would probably want to rectify a dulling system within the first five flips. While S(11) has a plateau of stability, once it starts to fall off any memory of its initial state will quickly be erased.
Investigating Systems of Many Bulbs – S(101)
Encouraged by the increased period of stability in S(11) compared to S(3), Archie and Bella starts looking into even larger systems. Will a larger system forget its initial state similarly or differently after the plateau of stability? Looking at the plateau of stability for S(101), its guarantee of remaining bright, is 50 flips. For S(101) the atmosphere is an emergent property that is starting to stick better. Running the program to estimate probabilities now yields this.
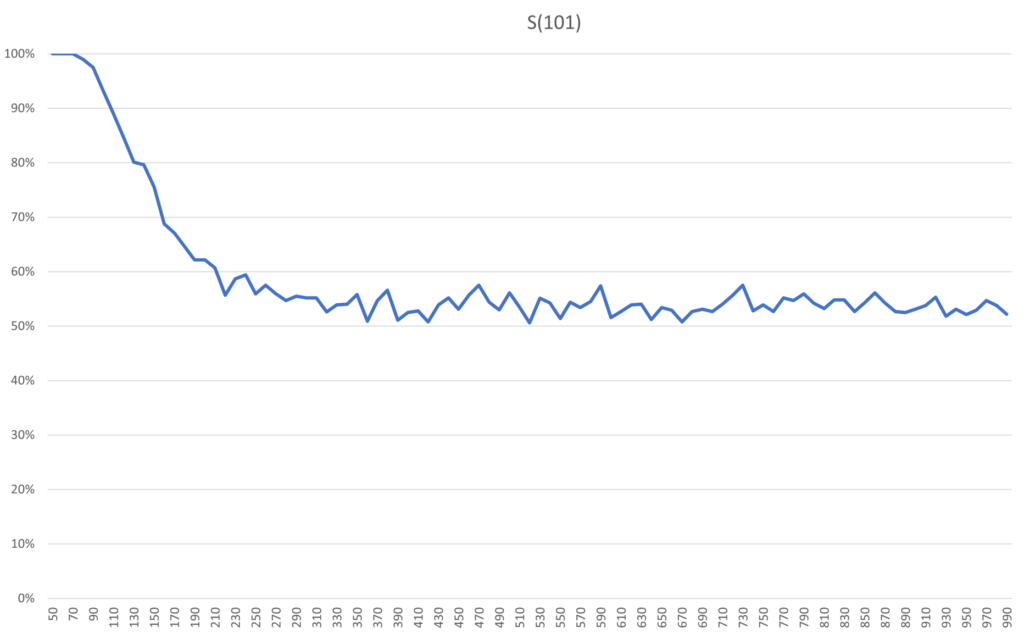
Relative the size of the system, the decline is just as steep here. In absolute numbers the decline happens over 100 flips, though, compared to 10 flips for S(11). In addition, the risk of dullness on the first flip after the guarantee in S(11) is 20%, whereas for S(101) and flip 51 it is very close to 0%. To reach 20% risk in S(101) you need around 130 flips. So if we can accept some risk, enlarging the system will extend the window in which we would have to take action to maintain a bright atmosphere. Also, the plateau of 0% or very close to 0% risk is extended here, up until about 80 flips.
Investigating Systems of Many Bulbs – S(100001)
The plateau of stability shown in S(11) and S(101) is something S(3) did not have. The extension of this plateau in S(101) is something S(11) did not have. Because of this, Archie and Bella wants to check a much larger system to both ensure that these features remain and if any new features can be seen. Pushing the program to its limits they test S(100001) and get these results.
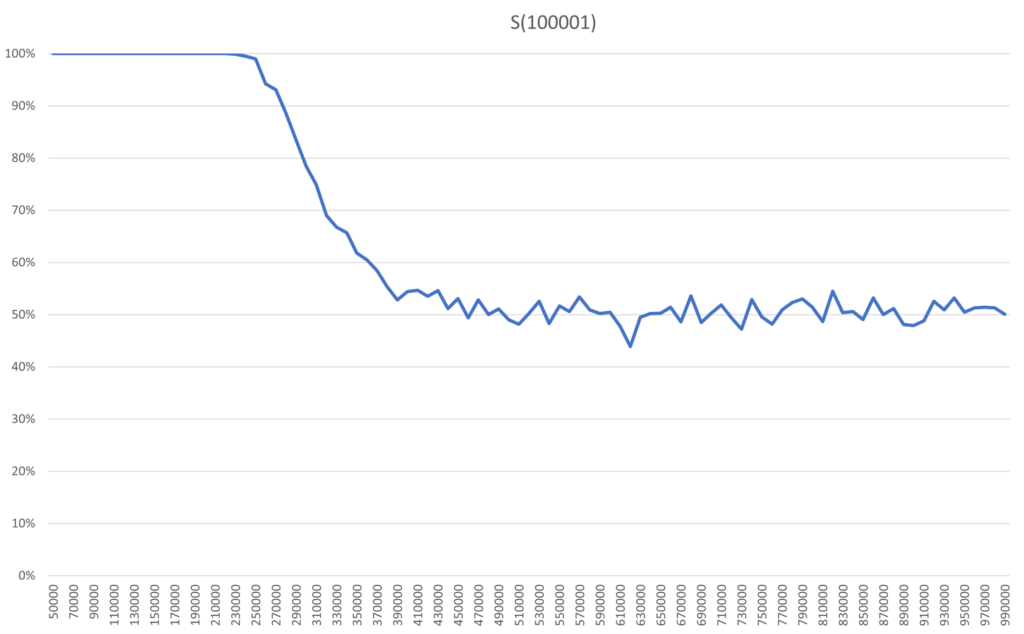
Relative the size of the model, the steepness of the decline during the erasure looks the same as before. In absolute numbers it is of course much longer than for the other systems, with about 150 000 flips for S(100001). The plateau is extended even further, so erasure starts later, after 230 000 flips. As a result, the risk of dullness is now 20% after about 300 000 flips. No new features can be seen here, so this graph likely captures how even larger systems will behave.
Remember that Archie and Bella set out to do the least amount of work to maintain a bright atmosphere. If the system is going to be susceptible to random disturbances or is affected by those using it, the system can be enlarged so much that the moment it would possibly reach dullness lies further into the future than the lifetime of the system itself. If that is an option, no work is required to ensure a bright atmosphere.
The Resilience of Emergence
It is in the mathematical nature of larger systems to provide better resilience for emergent properties like our defined atmosphere. However, once the decline sets in, such emergent properties can be erased relatively quickly. Coming back to large language models, I believe this is why we see them quickly gaining emergent properties, but only when models pass certain sizes. Taking one of those emergent properties and looking at a model below the threshold, it will not appear because erasure sets in before it can be properly established. Contrarily, once a model is large enough that an emergent property can survive on the plateau of stability, it will quickly establish itself.
Comparing the atmosphere of a system of many bulbs with the emergent properties of a large language model is of course a dramatic simplification, but I believe there are enough parallels between the two that some conclusions can be drawn. If the likeness is valid, the nature of the steep decline may provide a challenge for models that are fine-tuned during operation. There is no guarantee that such fine-tuning is not comparable to dulling a bright atmosphere for some of its emergent properties. The ability of GPT-4 to draw a unicorn may already be one such example.
I hope you enjoy this as much as the programmer friend of Archie and Bella did.
Unfortunately the images on this article from media.licdn.com are returning 403 for example: https://media.licdn.com/dms/image/D4D12AQHHb1dgDRLDag/article-inline_image-shrink_1000_1488/0/1687334398250?e=1692835200&v=beta&t=7NbiEYsJsc8g5NgTBlZT8RYGiBx5Cee48HBq9Ij9tUw
A cut and paste error on my part. I believe the images should be visible now. Thanks for pointing this out!
“The system is susceptible to random disturbances, making the bulb uncontrollably go on or off.”
This language causes some difficulty, as it seems to assume that “randomness” can be the *cause* of something.
Something always causes the bulb to go on or off, and that something is “unknown” – which sometimes is used as a synonym for “random”.
Coin flips, for example – with an accurate enough physical device, you can flip a coin and have a complete certainty which side the coin will land on. You can *model* the relative frequency of the system, but that model is not reality – “randomness” is not a cause, “probability” is not a cause. And the relative frequency is not the probability.
“But what if the system is susceptible to random disturbances?” That’s only “random” based on the assumption that the complete set of ‘unknown causes’ is basically a bunch of coin flips. What makes that model better than another model?
For the sake of this example, I used a (pseudo) random number generator to investigate the resilience of an emergent property in a system. My references to “randomness” should be taken in that context. If we look at LLMs in particular and when an unexpected property emerges, I was interested in understanding if there is any mathematical reason for it to gain resilience and persist even if the model undergo changes.
When it comes to randomness being the cause, I believe it’s still debatable whether irreducible randomness exists or not. If we assume that it does and is possible to tap into, we could use that as a source for a bulb switch controller. Following a causality chain in such a setup will then ultimately lead us to that source.